Ratings

Tournaments in Australia are rated in the national system provided they meet ratabilty criteria The algorithm is an adapted version of Elo Ratings
You can inspect the list of players ranked by rating:

RATING.DAT and ratings software for tournament organisers here

Criteria for inclusion

Generally, a tournament will be rated if it meets the criteria of a standard tournament. Non-standard tournaments may still be rated if they are approved for rating by CASPA on the recommendation of advisers appointed.

CASPA has the right to veto the rating of any tournament, either before or after the event, which fails to meet the criteria. Internet and handicapped tournaments will not be rated by the national system.

STANDARD TOURNAMENT
A standard tournament is defined by the following

  1. RULES. ASPA Rules of Tournament Play (with State variations) and the “basic” rules are to apply unless specified in advertising.
  2. NUMBER OF GAMES A tournament will have a minimum of 4 games.
  3. NUMBER OF PLAYERS PER GAME All games are to be played with two competitors.
  4. TOTAL NUMBER OF PLAYERS. A tournament will have a minimum of six players. If the number of players falls below six, subsequent games are not rateable.
  5. TIME Each game is to allow a minimum of 18 minutes playing time per player. The maximum time allowed is 25 minutes per player per game.
  6. ELIGIBILITY A tournament will be open to all players. Minimum or maximum ratings may be required.
  7. FORMAT OF DRAW Player pairings will be by objective and systematic means. (eg round robin, king of the hill, AuPair etc)
  8. ADVERTISING
    1. Tournament advertising must take place at least two weeks prior to the event at both national and state levels, and must include date, venue and contact information.
    2. National advertising must include listing on the national website tournament calendar.The following advertising mechanisms are available: Across The Board (National), Scrabble Australia website, Scrabble Australia email list, notices sent to clubs or members in the State, Announcements and notices at prior tournaments, State Website
    3. State advertising should include details of the number and length of games, and tournament format.
NON-STANDARD TOURNAMENT
A tournament is non-standard if it varies in any aspect from the criteria listed above under “Standard Tournament”.
A non-standard tournament will only be rated if it receives approval by CASPA. Approved variations to a standard tournament will be specified in all advertising.
Last reviewed: June 2009

Scope


After a player has competed in their first official tournament, they will be assigned a player rating. This rating will be adjusted after each tournament that the player takes part in from then on. Ratings are used to divide players into tournament Sections. They are also used to set minimum ability levels at major tournaments and for selection of representative teams. Players like to track their rating to monitor progress or set goals.
In Australia, our National Ratings System includes players from all States. Dormant players, overseas players and players not belonging to one of the State Associations may be removed without notice.
The National Ratings System updates a National Ratings file, a text file called RATING.DAT with rating information for each player. A typical line in RATING.DAT looks like this
2013 WA Geoff Shepheard 1113 1483 20241006
where 2013 is the year that they first played, WA is the player's state, 1113 is the number of rated games, 1483 is their current rating, 20241006 is 2024 Oct 6, which is the date the player last played in a rated tournament.

How It Works


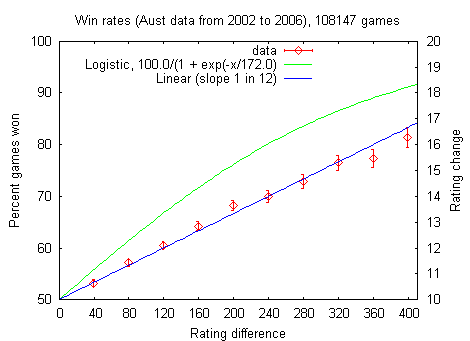
Ratings curve
The rating system is essentially the Elo rating system. At the heart is a rule which models the probability that a higher rated player will beat a lower rated player. The curve is a function of the difference in ratings. Prior to Dec 1, 2006, Australia used a logistic curve with a slope parameter of 172. The formula (expressed in spreadsheet language) is 1/(1 + EXP(-x/172)). However checking the actual win rates using many games shows that the curve is wrong.
For instance when the ratings difference is 300, the logistic formula gives the higher rated player an 85% chance of winning, but the data show that they win only 74% of such games.

In 2010 we introduced a straight line rule which better accords with the prior data. Your percent chance of winning is fifty plus one twelfth of the rating difference (but capped at 95%).

The practical consequences are that the higher rated players in a section will find it fairer in maintaining their rating, or being able to progress to the next higher sectionif they can prove their worth.

It was expected that atings would slowly change as the result of the change, and it is possible that we may again get a mismatch between the observed win proportions and the modelled probability. Monitoring has occured from time to time, but no changes have been recommended.

Here is an example of how you can calculate your rating change.

Example: You are rated 1453. You win 5 out of 7 games against opponents whose average rating is 1393.

  1. You are 14553- 1393 = 60 points higher on average.
  2. Your calculated probability of winning a game is on average = 50 + 1/12 of 60 = 55%.
  3. You would be expected to win 55% of the 7 games, ie 3.85 games.
  4. You actually won 5 games, which is +1.15 games better than expected.
  5. A multiplier of 20 usually applies1. Your rating gain is 1.15 x 20 = 23 points
1. A multiplier will effectively be larger than 20 for a provisional player. Players new to our rating system are deemed provisional until they have 50 rated games. Their first few tournaments are in effect treated as one big tournament. This smooths out fluctuations and will allow them to rise more rapidly if they improve during the provisional period.

The source code in Perl can be downloaded by right clicking here.
Revised 3 July 2022 to include info previously found on other pages.
Revised 26 Apr 2023 to use classless stylesheet.
Revised 15 Oct 2024 to explain first field in RATING.DAT is beginning year (was eg GSHE)